On-Going Research
Scientific Machine Learning – Physics Informed Networks
FastVPINNs – A Tensor-driven accelerated hp-variational PINNs framework for complex geometries
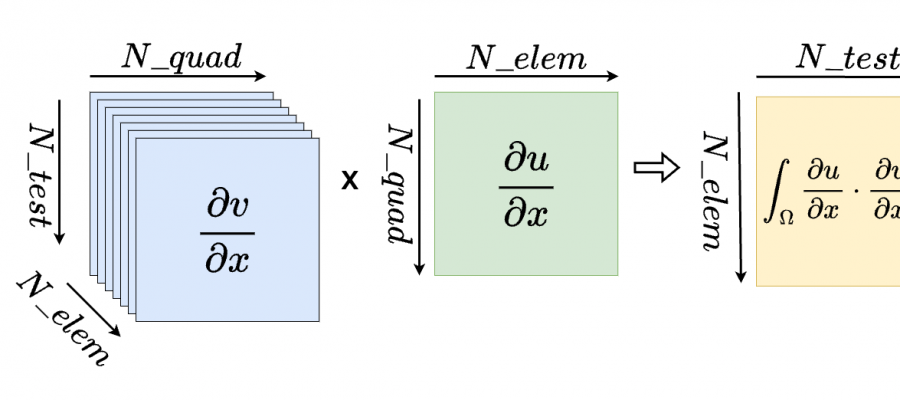
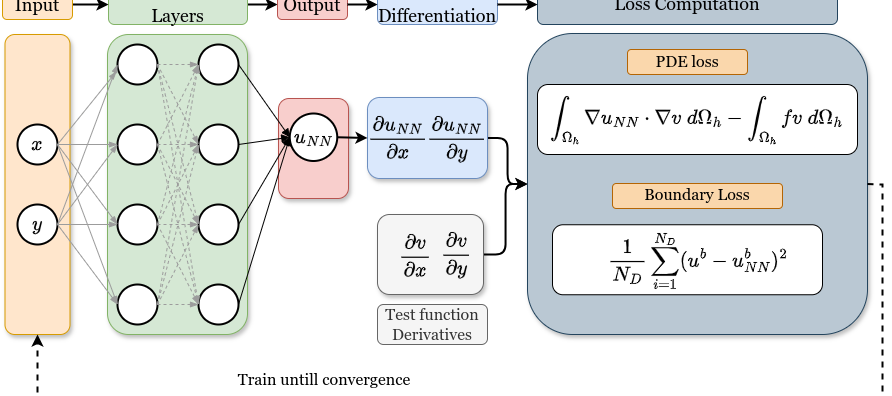
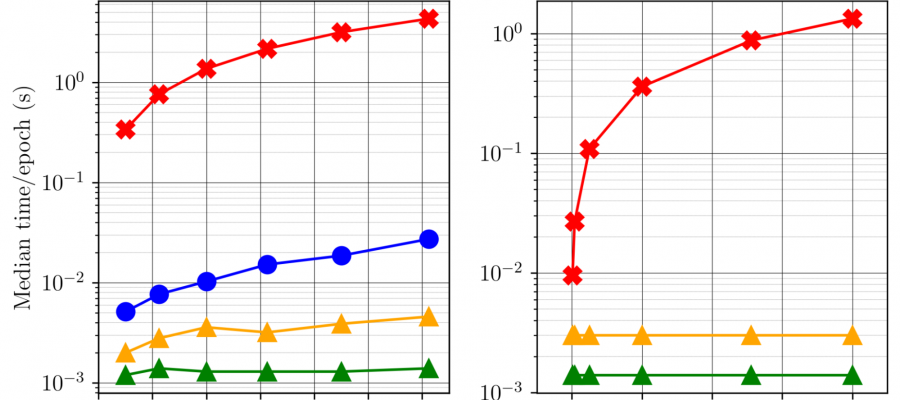
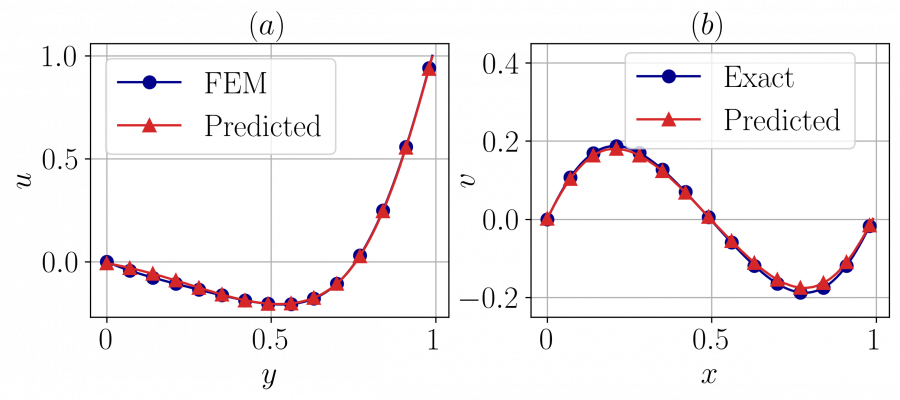
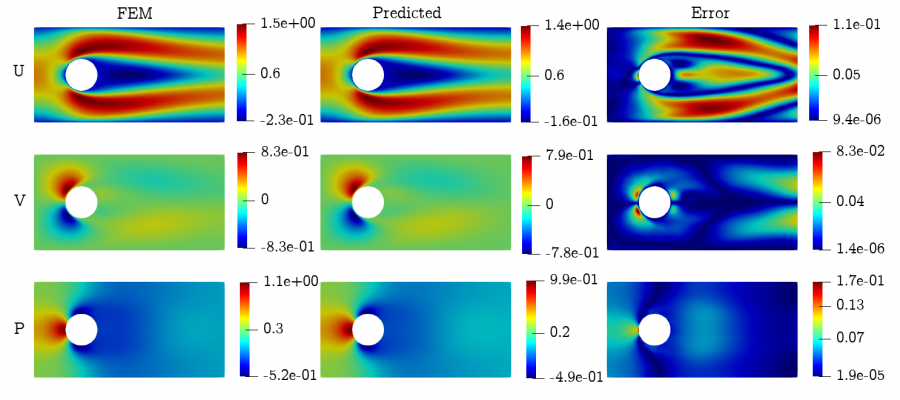
Variational Physics-Informed Neural Networks (VPINNs) utilize a variational loss function to solve partial differential equations, mirroring Finite Element Analysis techniques. Traditional hp-VPINNs, while effective for high-frequency problems, are computationally intensive and scale poorly with increasing element counts, limiting their use in complex geometries. This work introduces FastVPINNs, a tensor-based advancement that significantly reduces computational overhead and handles complex geometries. Using optimized tensor operations, FastVPINNs achieve a 100-fold reduction in the median training time per epoch compared to traditional hp-VPINNs. With proper choice of hyperparameters, FastVPINNs can surpass conventional PINNs in both speed and accuracy, especially in problems with high-frequency solutions. Demonstrated effectiveness in solving inverse problems on complex domains underscores FastVPINNs’ potential for widespread application in scientific and engineering challenges, opening new avenues for practical implementations in scientific machine learning.
Topics: Scientific Machine Learning, Physics Informed Neural Networks
People: Thivin Anandh, Divij Ghose, Himanshu Jain, Prof. Sashikumaar Ganesan
ArXiV link to Paper : https://arxiv.org/abs/2404.12063
Python PIP Library for FastVPINNs
The existing implementation of hp-VPINNs framework suffers from two major challenges. One being the inabilty of the framework to handle complex geometries and the other being the increased training time associated with the increase in number of elements within the domain. In the work , we presented FastVPINNs, which addresses both of these challenges. FastVPINNs handles complex geometries by using bilinear transformation, and it uses a tensor-based loss computation to reduce the dependency of training time on number of elements. The current implementation of FastVPINNs can acheive an speed-up of upto a 100 times when compared with the existing implementation of hp-VPINNs. We have also shown that with proper hyperparameter selection, FastVPINNs can outperform PINNs both in terms of accuracy and training time, especially for problems with high frequency solutions.
Our FastVPINNs framework is built using TensorFlow-v2.0, and provides an elegant API for users to solve both forward and inverse problems for PDEs like the Poisson, Helmholtz and Convection-Diffusion equations. With the current level of API abstraction, users should be able to solve PDEs with less than six API calls as shown in the minimal working example section. The framework is well-documented with examples, which can enable users to get started with the framework with ease.
The ability of the framework to allow users to train a hp-VPINNs to solve a PDE both faster and with minimal code, can result in widespread application of this method on several real-world problems, which often require complex geometries with a large number of elements within the domain.
Link : https://github.com/cmgcds/fastvpinns
Topics: Scientific Machine Learning, Physics Informed Neural Networks, Python, CI/CD
People: Thivin Anandh, Divij Ghose, Prof. Sashikumaar Ganesan

hp-Variational Physics Informed Neural Networks for Incompressible Navier-Stokes equations
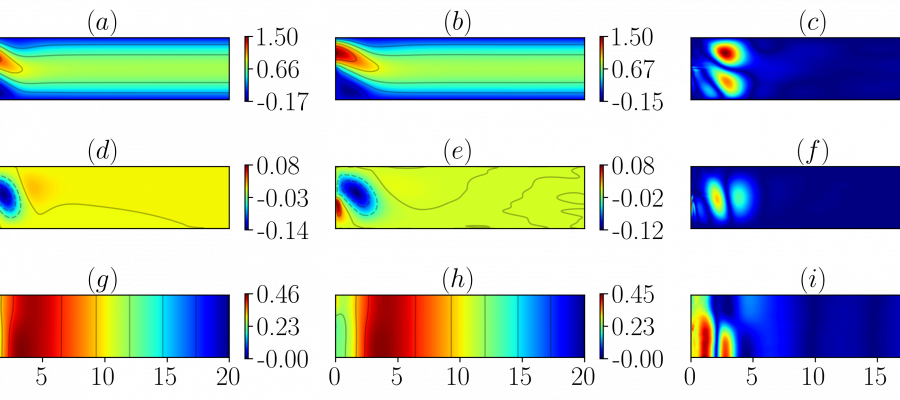
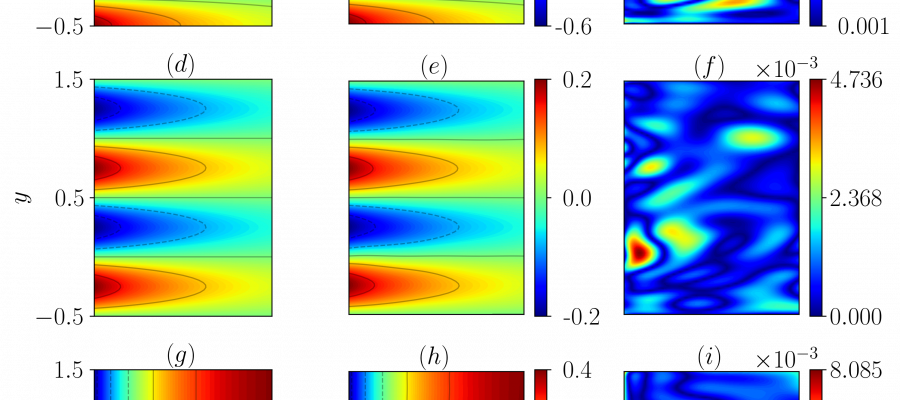
Following the successful implementation of FastVPINNs to address the training time complexity in hp-VPINNs, we have extended the framework to accommodate vector-valued problems. We also solved the Incompressible Navier-Stokes equations for problems including lid-driven cavity flow and flow past a backward-facing step. Additionally, we have applied this methodology to inverse problems involving the Navier-Stokes equations, specifically for the determination of the Reynolds number in fluid flows in the Laminar Region. Our comparative analysis demonstrates that for certain flow configurations, FastVPINNs exhibits a twofold decrease in training time compared to traditional PINNs, while maintaining equivalent accuracy in results.
Topics: Scientific Machine Learning, Variational Physics Informed Neural Networks
People: Thivin Anandh, Divij Ghose, Prof. Sashikumaar Ganesan
A Deep Learning Simulation Framework for Building Digital Twins of Wind Farms: Concepts and Roadmap
Simulation-based Digital Twins are often limited by the difficulties encountered in the real-time simulation of continuous physical systems, for example, fluid flow simulations in complex domains. Classical methods used to simulate such systems, such as the mesh-based methods, typically require state-of-the-art computing infrastructure to get a rapid estimation of the trajectory of the system dynamics if the problem size is large. We propose a simulation framework comprising of a Physics Informed Neural Network (PINN) and a model order reduction strategy based on the Dynamic Mode Decomposition (DMD) technique for rapid simulation of fluid flows, such as air, in complex domains. This framework is primarily targeted at realizing a Digital Twin of a wind farm in terms of the aerodynamics aspects. However, the framework will be flexible and capable of creating simulation-based Digital Twins of other systems involving continuous physics.
Topics: Scientific Machine Learning, Physics Informed Neural Networks, Scientific Machine Learning
People: Subodh Joshi, Thivin Anandh, Prof. Sashikumaar Ganesan
AI For Defence
This project focuses on developing an advanced machine learning (ML) system designed to integrate and optimize multiple ML models for complex defense and surveillance applications. This system encompasses the design and implementation of models for signal clustering, emitter classification, and AI-based multi-sensor data fusion, including the integration of sensor outputs from different types of sensors for enhanced detection, classification, localization, and tracking. Additionally, it addresses voice command and radio intercept analysis, target detection, and includes a end-user associate application. We emphasize optimizing these ML models for high accuracy, adaptability, and real-time performance, while also implementing MLOps principles to streamline development, deployment, and ongoing monitoring.
People: Prof. Sashikumaar Ganesan, Lokesh Mohanty, Protyush Pradyut Chowdury
High Performance Computing & Computational Fluid Dynamics
GPU Accelerated Lagrangian Particle deposition in Human Air pathway
Efficient particle deposition modeling is crucial for understanding regional particle deposition effects on human airways. Lagrangian particle tracking in large, complex domains presents two primary challenges: high computational costs and the requirement for a robust framework with effective interpolation routines and comprehensive mesh information. Finite Element Method (FEM) routines, utilized for fluid modeling, are ideal due to their interpolation capabilities and data structures, which store mesh and geometric information essential for tracking and identifying particle deposition status. However, FEM data structures are complex and usually reside on CPUs, making it challenging to port them to GPUs. Despite this, GPUs offer significant parallelization potential for particle tracking if these data structures can be efficiently managed. In this work, we introduce a GPU-accelerated Lagrangian particle deposition framework utilizing FEM-based routines. Our approach focuses on efficient transfer and simplification of FEM data structures from CPU to GPU, facilitating the implementation of zonal-based particle searching and inertial deposition techniques directly on the GPU. Our model demonstrated lower sequential execution time than ANSYS Fluent’s particle tracking module and achieved a 100x speedup over the Sequential CPU implementation and a 4x speedup over the OpenMP implementation for number of particles up to 5 Million. The GPU-accelerated framework reduces execution time from days to hours for complex geometries, enabling deeper exploration of particle deposition in human airways.
Topics: GPU Programming, Turbulence Modelling, Finite Element Method
People: Thivin Anandh, Lokesh Mohanty, Prof. Sashikumaar Ganesan
Physics Informed Meshing
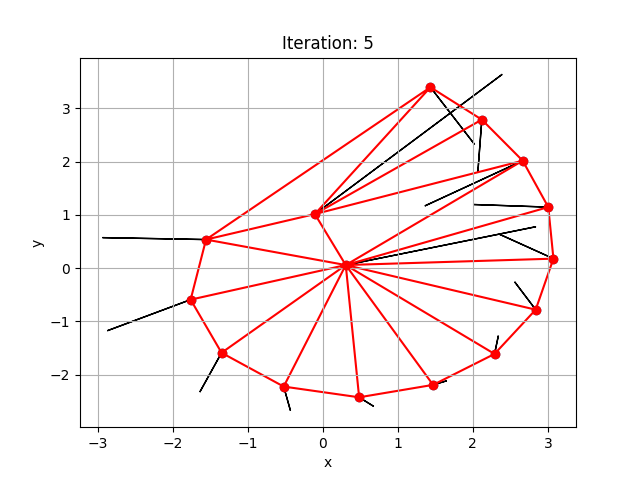
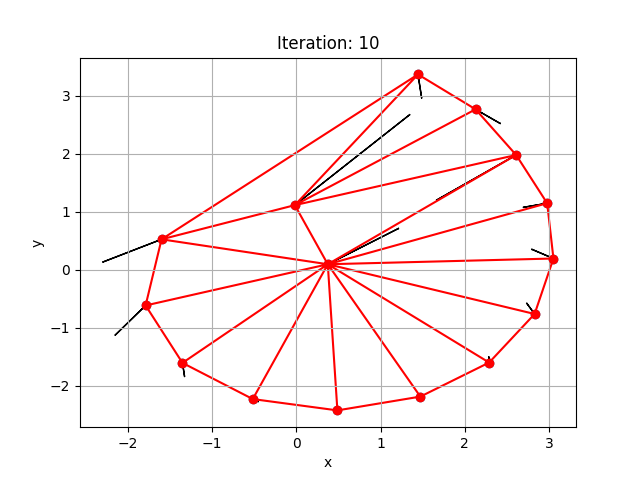
We wish to devise physics-informed iterative schemes to find optimum meshes for Computational Fluid Dynamics (CFD) problems. Preliminary work has begun for Poisson’s problem in two dimensions and is being built over TensorFlow v2.26.1 and the Triangle v20230923 packages in Python v3.11.9.
The figures illustrate the moving of a mesh to minimise a simple objective function, that is the variance in the area of the triangular elements of the given mesh. The red lines show the boundaries of mesh elements. The black lines show the direction the nodes of the mesh must move according to the gradient descent method to minimise the objective function.
People: Rajarshi Dasgupta, Prof. Sashikumaar Ganesan
Completed Work
High Performance Computing ( GPU Programming )
Parallel Smoothers for Multigrid Method in heterogeneous CPU-GPU environment
In our research, we developed hybrid parallel smoothers for the geometric multigrid method to efficiently solve systems of equations. We compared various hybrid parallel approaches, including GPU-only, alternating GPU-CPU, and a novel combined GPU-CPU approach, against an MPI-only implementation. The first part of our work focused on Jacobi and Gauss-Seidel smoothers for solving the Poisson equation, utilizing a coloring strategy to parallelize operations on GPU and implementing CSR Scalar and CSR Vector techniques for sparse matrix-vector multiplication. We studied the strong scaling behavior across various parameters. The second part addressed Vanka-type smoothers for saddle-point problems arising from the Navier-Stokes equation, where we accelerated the assembly of local systems using hybrid parallel approaches and developed a coloring strategy for independent cells or pressure degrees of freedom. We offloaded the task of determining cell or DOF neighbors to GPU and parallelized the solving of local systems using OpenMP on CPU. Throughout both parts of the work, we conducted extensive experiments to study strong scaling results across different problem sizes, number of OpenMP threads, and multigrid types, providing a comprehensive analysis of our hybrid parallel smoothing techniques for geometric multigrid methods.
Topics: Multigrid Solvers, Finite Element Method, GPU Programming
People: Neha Iyer, Prof. Sashikumaar Ganesan
SParSH-AMG: A library for hybrid CPU-GPU algebraic multigrid and preconditioned iterative methods
Hybrid CPU-GPU algorithms for Algebraic Multigrid methods (AMG) to efficiently utilize both CPU and GPU resources are presented. In particular, hybrid AMG framework focusing on minimal utilization of GPU memory with performance on par with GPU-only implementations is developed. The hybrid AMG framework can be tuned to operate at a significantly lower GPU-memory, consequently, enables to solve large algebraic systems. Combining the hybrid AMG framework as a preconditioner with Krylov Subspace solvers like Conjugate Gradient, BiCG methods provides a solver stack to solve a large class of problems. The performance of the proposed hybrid AMG framework is analysed for an array of matrices with different properties and size. Further, the performance of CPU-GPU algorithms are compared with the GPU-only implementations to illustrate the significantly lower memory requirements.
Topics: Algebraic Multigrid Solvers, Finite Element Method, GPU Programming
People: Manan Shah, Prof. Sashikumaar Ganesan
Computational Fluid Dynamics
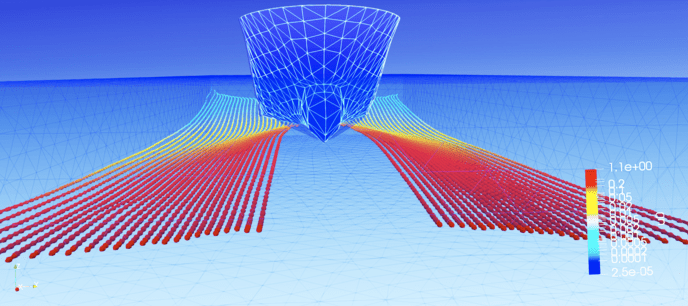
Ship Hydrodynamics
This project was done with collaboration from Naval Research Board, India on generating the robust computational methods for solving problems related to Ship Hydrodynamics.
Topics: Finite Element Method, Computational Fluid Dynamics
People : Thivin Anandh, Bhanu Teja, Prof. Sashikumaar Ganesan
Scientific Machine Learning
On the choice of hyper-parameters of artificial neural networks for stabilized finite element schemes
This work provides guidelines for an effective artificial neural networks (ANNs) design to aid stabilized finite element schemes. In particular, ANNs are used to estimate the stabilization parameter of the streamline upwind Petrov–Galerkin (SUPG) stabilization scheme for singularly perturbed problems. The effect of the artificial neural network (ANN) hyper-parameters on the accuracy of ANNs is found by performing a global sensitivity analysis. First, a Gaussian process regression metamodel of the artificial neural networks is obtained. Next, analysis of variance is performed to obtain Sobol’ indices. The total-order Sobol’ indices identify the hyper-parameters having the maximum effect on the accuracy of the ANNs. Furthermore, the best-performing and the worst-performing networks are identified among the candidate ANNs. Our findings are validated with the help of one-dimensional test cases in the advection-dominated flow regime. This study provides insights into hyper-parameters’ effect and consequently aids in building effective ANN models for applications involving nonlinear regression, including estimation of SUPG stabilization parameters.
Topics: Scientific Machine Learning, Finite Element Method, Singularly Perturbed Problems
People: Subodh Joshi, Thivin Anandh, Bhanu Teja, Prof. Sashikumaar Ganesan
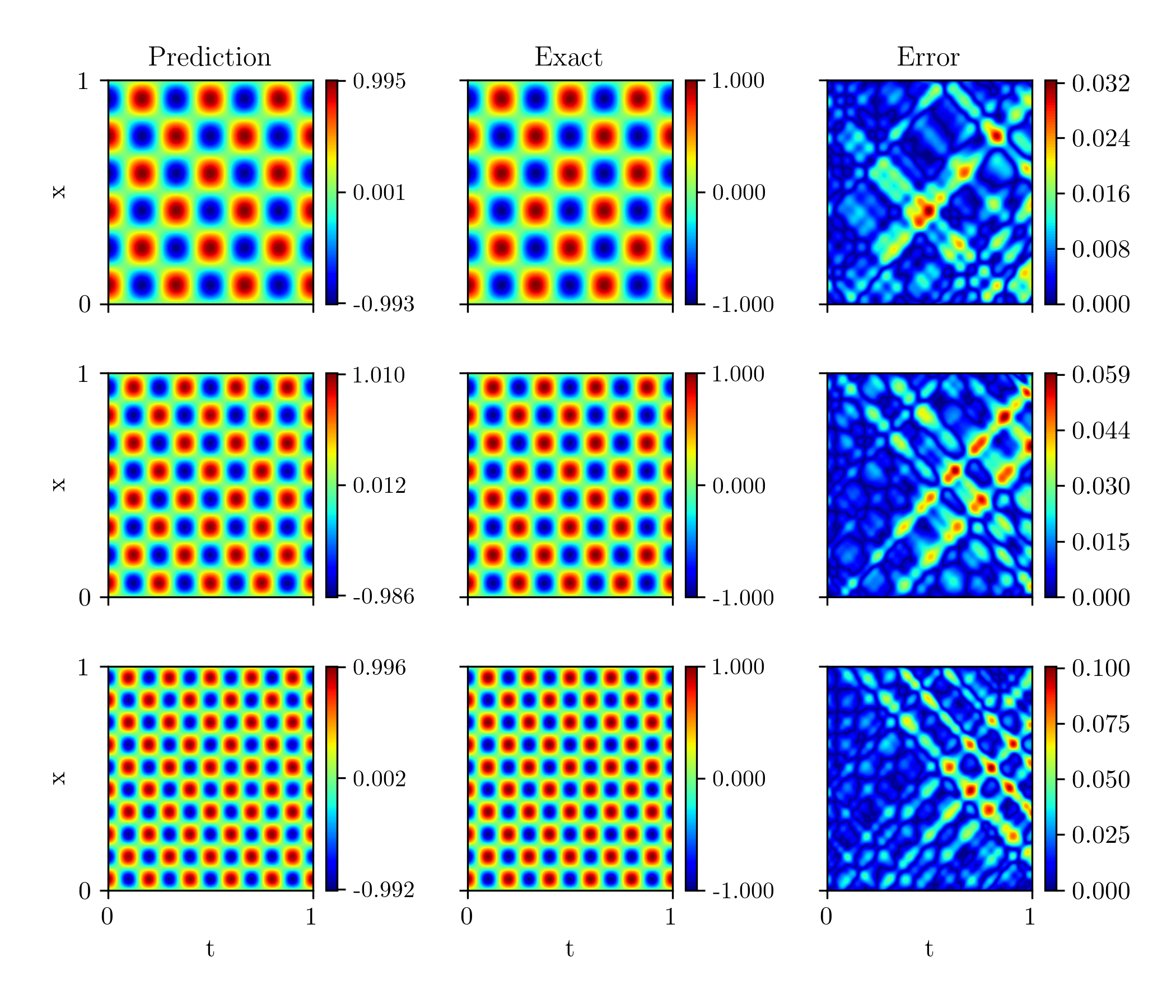
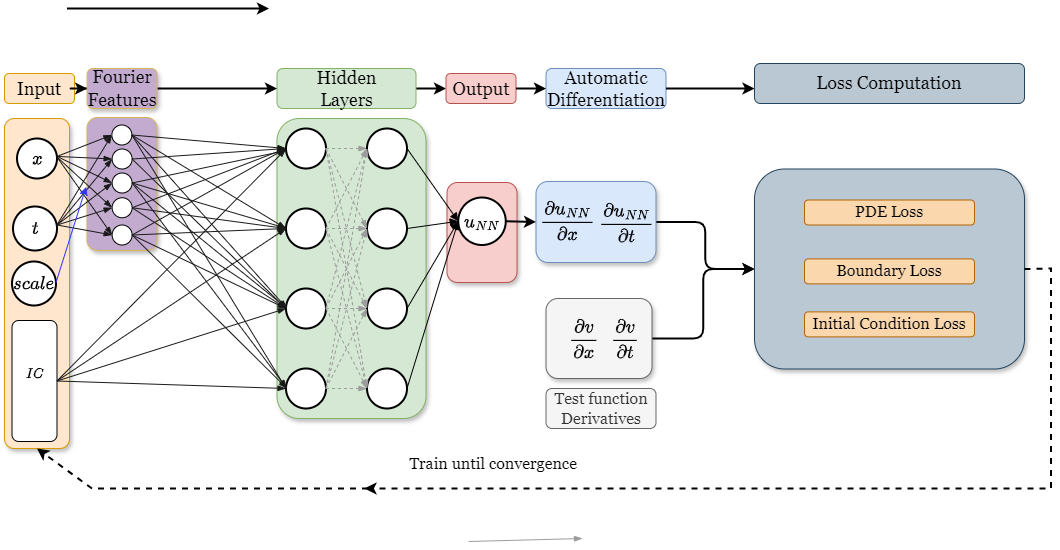
Learning multiple initial conditions using PINNs and VPINNs
The current state of development in the application of physics informed neural networks and their extensions has made them a necessity in solving differential equations. Most of the existing strategies are concerned with individual initial/boundary conditions. As for the focus of this study, it handles one-dimensional, time-dependent problems and multiple initial value problems within a single network. We improve the degree of convergence for high-frequency problems and extend it to the FastVPINNs structure to solve a set of initial value problems utilizing VPINNs. Lastly, we demonstrate an ablation study for understanding how various initial value problem is learned from the parameters of the network.
People: Mahesh Tom, Prof. Sashikumaar Ganesan